
The result for polygonal paths shows that the straight line between the endpoints is the shortest of all the polygonal approximations. By definition, the arc length of a curve is the least upper bound of the lengths of all polygonal approximations of the curve. A summary of definitions, postulates, algebra rules, and theorems that are often used in geometry proofs: Definitions: Definition of mid-point and segment. This implies that no curve can have an arc length less than the distance between its endpoints.

No polygonal path between two points is shorter than the line between them. Postulate 17 The area of a square is the square of the length of a side (A s 2) Postulate 18 (Area Congruence) If two figures are congruent, then they have the same area. This generalization can be used to prove that the shortest curve between two points in Euclidean geometry is a straight line. Postulate 16 (Arc Addition) The measure of the arcs formed by two adjacent arcs is the sum of the measures of these two arcs. The arc length of a curve is defined as the least upper bound of the lengths of polygonal approximations. Consequently, r is limited to the range 1/ t < r < t where t is the tribonacci constant. The left-hand side polynomials of these two inequalities have roots that are the tribonacci constant and its reciprocal.

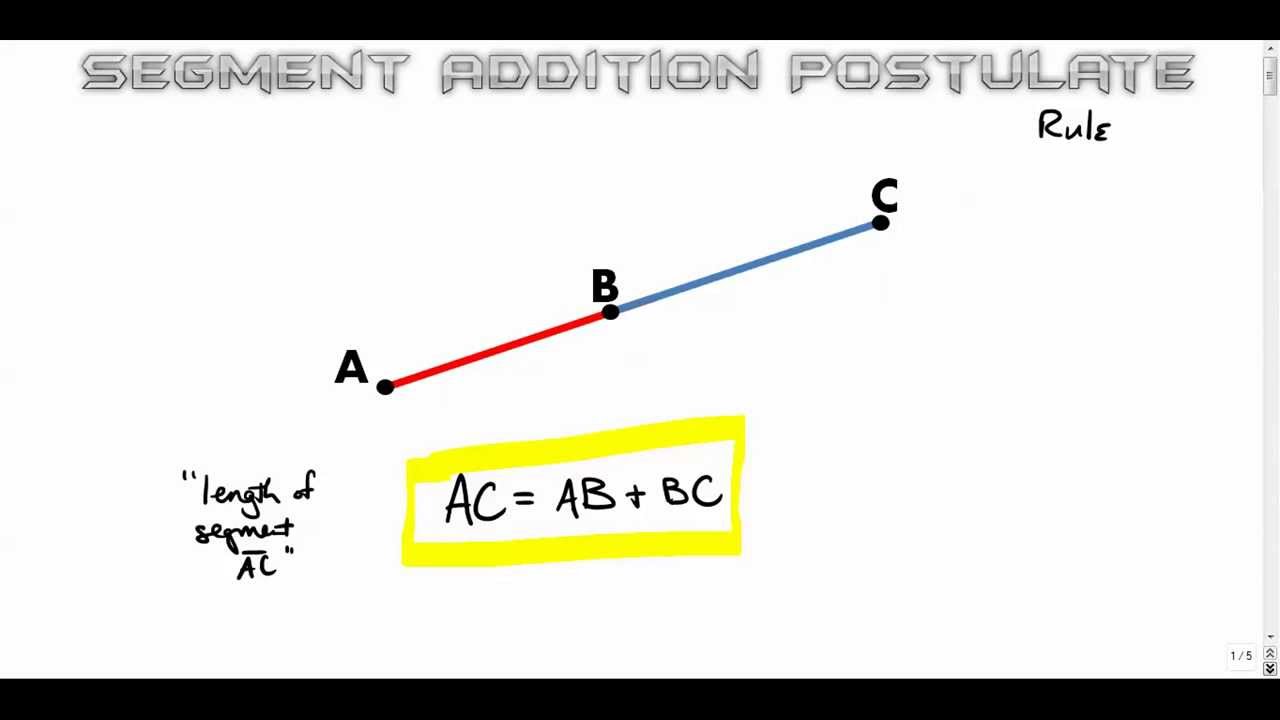
In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths ( norms): The Segment Addition Postulate is similar to the angle addition postulate, but you are working with line segments instead of adjacent angles. That is, the measure of the larger angle is the sum of the measures of the two smaller ones. With equality only in the degenerate case of a triangle with zero area. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that A major arc is the longer arc connecting two endpoints on a circle. The measure of a minor arc is less than 180 °, and equal to the measure of the arcs central angle. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. Arcs A minor arc is the shorter arc connecting two endpoints on a circle. In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. The top example shows a case where z is much less than the sum x + y of the other two sides, and the bottom example shows a case where the side z is only slightly less than x + y. Three examples of the triangle inequality for triangles with sides of lengths x, y, z.


 0 kommentar(er)
0 kommentar(er)
